معرفی مفاهیم کلیدی علم آمار

ازآنجاکه مفاهیم و ابزارهای آماری نقش مفید و مهمی در انجام انواع پژوهش‌ها ایفا می‌کنند، دانستن این مفاهیم برای کسی که با آمار سرکار دارد ضروری است. در این مقاله به بررسی معرفی مفاهیم کلیدی علم آمار و کاربرد هر کدام از آنها می‌پردازیم.

مفاهیم کلیدی علم آمار نقش مفید و مهمی در انجام انواع پژوهش‌ها ایفا می‌کنند. در کل، این مفاهیم در نوشتن انواع مختلف مقالات علمی کاربرد دارند. بنابراین، دانستن این مفاهیم برای کسی که با آمار سرکار دارد ضروری است. در ادامه به بررسی معانی این مفاهیم می‌پردازیم.

• جامعه یا جمعیت آماری (Statistical population)

یکی از مفاهیم اولیه و پایه ای علم آمار جمعیت آماری است. به گروه یا طبقه از افراد یا اشیاء که حداقل یک ویژگی مشترک دارند جامعه آماری گفته می‌شود. در حالت معمول، به بررسی کل اعضای جامعه آماری سرشماری می‌گویند؛ اما ازآنجایی‌ که سرشماری به‌ وقت و هزینه بالایی نیاز دارد، در برخی مواقع فقط نمونه خاصی از جامعه آماری را مورد مطالعه قرار می‌دهند. تعداد اعضای جامعه را اندازه جامعه نامیده می‌ شود که با حرف N نشان می‌دهند. هر یک از اشیاء جامعه، یک فرد جامعه است. جامعه را می‌توان بر اساس معیارهای مختلفی مثل نوع جامعه (مانند جامعه انسانی، جامعه گیاهی و...) و یا تعداد اعضای جامعه دسته‌ بندی کرد.

جامعه آماری

• طبقه‌ بندی کلی جامعه آماری

جامعه موردنظر: یا جامعه هدف، جامعه‌ ای است که علاقه داریم پژوهش‌های خود را به آن تعمیم دهیم. جامعه هدف می‌تواند متشکل از اعضای واقعی یا فرضی باشد.

جامعه مورد مطالعه: جامعه مورد مطالعه به بیان ساده جامعه‌ ای است که در عمل مورد بررسی قرار می‌ گیرد.

جامعه در دسترس و جامعه نمونه: در مطالعه می‌توان همه اعضا جامعه یا نمونه جامعه موردنظر را مورد بررسی قرار داد. به جامعه‌ ای که همه اعضا آن را مورد مطالعه قرار دهیم جامعه در دسترس و به جامعه ای که فقط نمونه خاصی از آن را بررسی کنیم جامعه نمونه گفته می‌شود.

• نمونه آماری (statistical sample)

یکی دیگر از مفاهیم کلیدی علم آمار نمونه آماری است. طبق تعریف، نمونه آماری به تعدادی خاص از اعضای جامعه گفته می‌شود که معمولاً به دلیل صرفه‌جویی در زمان و هزینه به شکل تصادفی از کل جامعه آماری انتخاب می‌شود.

بررسی و مطالعه نمونه‌ها باید با احتیاط خاصی انجام شود. چرا که در تمام روش‌های نمونه‌گیری، احتمال خطایی اجتناب‌ ناپذیر وجود دارد. به‌ طورکلی هرچقدر تعداد اعضاء نمونه‌ها به تعداد اعضاء جامعه آماری نزدیک‌ تر باشد خطای اندازه‌ گیری کمتر است.

• نمونه‌ گیری (sampling)

نمونه‌ گیری یکی از ارکان مهم علم آمار است و به‌ منظور گرد آوری داده‌ های مورد نیاز درباره افراد جامعه انجام می‌شود. در نمونه‌ گیری هرچقدر که تعداد و تنوع نمونه‌ها زیاد باشد نتایج قابل‌ اعتمادتر است.

به‌ طورکلی به دو روش سرشماری و نمونه‌ گیری می‌ توان اطلاعات را گردآوری کرد.روشهای نمونه گیری عبارتند از: 

• روش های نمونه گیری تصادفی
  •  نمونه‌گیری تصادفی ساده (Simple Random Sample)
  • نمونه‌گیری سیستماتیک (Systematic Sampling)
  • نمونه‌گیری طبقه‌ای (Stratified Sampling)
  • نمونه‌گیری خوشه‌ای (Cluster Sampling)
• روش نمونه گیری غیرتصادفی
  • نمونه گیری گلوله برفی (snowball sampling)
  • نمونه گیری اتفاقی (Accidental Sampling)
  • نمونه گیری متوالی (Consecutive Sampling)
  • نمونه گیری قضاوتی (Judgmental Sampling)

• آماره (statistics) و پارامتر (parameter)

پارامترها، اندازه‌ گیری‌هایی عددی و معمولاً نامعلوم هستند که ویژگی‌های یک جمعیت آماری را بیان می‌کنند. معمولاً پارامترها برای برآورد جامعه آماری مؤثر هستند و ازآنجایی‌ که مقداری نامعلوم دارند دقیق نیستند. به طور قراردادی پارامترها را با حروف یونانی نمایش می‌ دهند.

از طرف دیگر، آماره‌ها نیز به‌عنوان برآوردگر پارامتر جامعه استفاده می‌ شوند و اندازه گیری هایی هستند که ویژگی های یک نمونه آماری را بیان می‌کنند. آماره‌ها با حروف لاتین نمایش داده می‌ شوند.

مقایسه آماره با پارمتر

• داده (Data)

داده‌ها را به‌ طورکلی، می‌توان همه دانسته‌ها، آگاهی‌ها، داشته‌ها، آمارها، شناسه‌ها، پیشینه‌ها و پنداشته‌ها نامید. داده‌ها یکسری اطلاعات خامی هستند که پیش از اینکه تبدیل به چیزهای مفید شوند نیازمند فرایندها و مراحلی خاصی هستند. داده‌ها شکل‌های مختلفی دارند مانند اعداد، حروف، نمادها وغیره

• متغیر (Variable)

متغیر از نظر لغوی به معنی چیزی است که تغییر می‌کند. در تحقیق نیز، متغیر به ویژگی‌هایی اطلاق می‌شود که می‌توان پس از مشاهده و اندازه‌ گیری دو یا چند عدد (به‌طورکلی ارزش و مقدار) را جایگزین آنها کرد. به‌عبارت‌ دیگر متغیرها عناصری هستند که محقق قصد اندازه‌گیری آنها دارد به همین دلیل ضروری است دیگران درک مشخصی از آن بر اساس تعریفی که محقق ارائه می‌ کند داشته باشند. مثلاً در پژوهش «بررسی میزان استرس امتحان و ارتباط آن با نمره امتحان دانش‌ آموزان»، موارد 1- میزان استرس امتحان و 2- نمره امتحان را می‌ توان جزو متغیرها دانست. در آمار متغیرها معمولاً با اصطلاح واریانس همراه هستند.

گاهی اوقات ممکن است ویژگی‌ هایی که در یک پژوهش اندازه‌ گیری می‌شوند، در پژوهش دیگر ثابت نگه‌ داشته شوند. ثابت به ویژگی‌هایی گفته می‌شود که دارای ارزش مساوی و یکسان هستند. به‌عنوان‌مثال، اگر در مثال بالا، دانش‌آموزان کلاس چهارم ابتدایی به‌عنوان آزمودنی به کار روند، «کلاس چهارم ابتدایی» ثابت می ‌باشد.

صفت مشخصه: صفاتی هستند که برای تمام افراد جامعه مشترک می‌باشند.

صفت متغیر: صفاتی می‌باشند که از یک فرد به‌ فرد دیگر جامعه تغییر می‌کند.

• انواع متغیرها

متغیرها با توجه به ماهیت متغیر و نقش متغیر در تحقیق به دو دسته اصلی تقسیم می شوند که در ادامه هر دسته به صورت خلاصه توضیح داده می شود.

طبقه بندی متغیرها برحسب ماهیت متغیر

برحسب ماهیت، متغیرها به سه گروه تقسیم می شوند: 

• متغیر کمی و کیفی
• متغیر گسسته و پیوسته
• متغیر دو ارزشی و چند ارزشی

متغیر کمّی (quantitative) و کیفی (qualitative)

متغیرهای کمّی، متغیرهایی هستند که می‌ توان برای آنها واحد و مبدأ اندازه گیری معین کرد، مانند قد، وزن، سن و غیره

متغیرهای کیفی را نمی‌توان جمع و تفریق کرد و در نتیجه برای آنها مبدأ اندازه گیری نیز وجود ندارد. برای مثال رنگ مو، رنگ چشم و جنس متغیرهای کیفی هستند.

متغیر گسسته (discrete) و پیوسته (continuous)

صفات کمی را می‌توان به دو بخش گسسته‌ و پیوسته تقسیم‌ بندی کرد. متغیر پیوسته، متغیری است که بین دو واحد آن نیز می‌توان نقطه با ارزشی انتخاب کرد. قد، زمان، طول یا ارتفاع پرش، درصد چاقی بدن و سطح هموگلوبین خون متغیرهای پیوسته هستند (یعنی اعشار پذیر هستند).متغیری که پیوسته نباشد، گسسته یا ناپیوسته است.متغیرهای گسسته فقط می‌توانند مقادیر عددی را بدون هیچ مقدار واسطه‌ ای ممکن، بپذیرند. به‌عنوان ‌مثال تعداد بازیکنان یک تیم فوتبال یک متغیر گسسته است، زیرا امکان ندارد مثلاً 7.5 بازیکن وجود داشته باشد. ناگفته نماند که به صورت نظری، شخیص بین متغیر پیوسته و گسسته امکان‌ پذیر نیست.

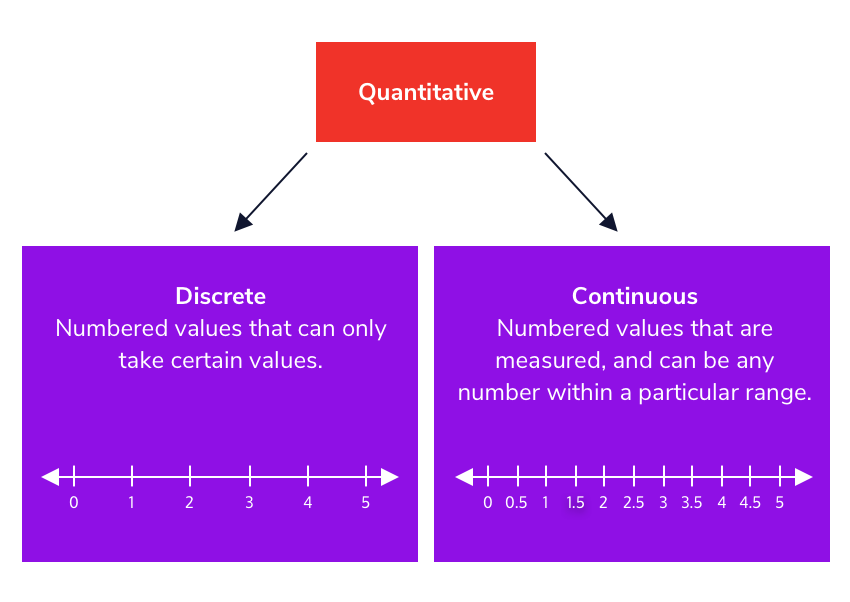
متغیر پیوسته و گسسته

• متغیرهای دو ارزشی و چند ارزشی

متغیرها را بر اساس مقادیر می‌توان به دو دسته دو ارزشی و چند ارزشی تقسیم‌ بندی کرد. متغیرهای دوارزشی متغیرهایی هستند که دو مقدار یا ارزش می‌توان برای آنها تعیین کرد. به‌عنوان‌مثال جنس زن و مرد.

از نظر کرلینجر (1986) متغیر دو ارزشی را شامل بخش‌های زیر هستند:

1- متغیرهای دوارزشی حقیقی (واقعی): این متغیرها دوبخشی واقعی هستند به‌عبارت‌ دیگر هر دو بخش به‌ صورت واقعی وجود دارند مانند زن و مرد، مرگ و حیات.

2- متغیرهای دوارزشی غیرحقیقی (ساختگی): که ویژگی‌های موردنظر آن، ساختگی و اعتباری است؛ مثل قبولی و مردودی

• طبقه‌ بندی متغیرها برحسب نقش متغیر در تحقیق

بر حسب نقش آنها در تحقیق، متغیرهای به انواع زیر تقسیم می شوند:

• متغیر وابسته

• متغیر مستقل
• مغیر تعدیل کننده
• متغیر کنترل
• متغیرهای مزاحم و ناخواسته
• متغیر وابسته (dependent variable)

متغیر وابسته متغیر ملاک است. با اندازه‌ گیری این متغیر تأثیر متغیر مستقل بر آن معلوم و مشخص می‌شود. محقق همواره قصد دارد این متغیرها به‌ صورت کمّی و سنجش پذیر درآورد.

به‌ عنوان‌ مثال، مدیری را در نظر بگیرید که از میزان فروش محصول جدید که پس از آزمایش بازار (ابزارسنجی) راضی نیست. متغیر وابسته در اینجا میزان فروش است. چون میزان فروش می تواند متفاوت باشد (میتواند کم، متوسط و زیاد باشد) ازاین‌ رو یک متغیر است، چون میزان فروش عامل اصلی مورد توجه مدیر است، پس متغیر وابسته است.

• متغیر مستقل (independent variable)

متغیر مستقل پیش‌ فرض متغیر وابسته است. به‌عبارت‌ دیگر این متغیر برای متغیر وابسته مانند یک مقدمه است و با این فرض متغیر وابسته نیز مانند یک نتیجه عمل می‌کند. از نظر برخی از اندیشمندان، اصطلاح متغیر وابسته و مستقل ویژه تحقیقاتی است که در آنها هدف، تبیین رابطه علت و معلولی میان متغیرهاست. توجه داشته باشید که امکان دارد متغیری که در یک مطالعه به‌عنوان متغیر مستقل عمل می‌کند، در مطالعه دیگر، متغیر وابسته باشد.

• متغیر تعدیل‌ کننده (moderator variable)

متغیر تعدیل‌ کننده رابطۀ مورد انتظار اصلی بین متغیرهای مستقل و وابسته را تغییر می دهد. به‌ عبارت‌ دیگر این متغیر بر رابطه متغیر مستقل و متغیر وابسته تأثیر اقتضایی دارد. البته امروزه این متغیر کاربرد چندانی ندارد. چراکه متغیرهای مستقل و وابسته به‌ قدری باهم تعاملی پیچیده دارند که تبیین پدیده‌ها از میان آنها کار بسیار دشواری است.

برای درک بیشتر این مفهوم فرض کنید محققی می‌خواهد تأثیر میزان مطالعه دانشجویان بر توان یادگیری آنان را بررسی نماید در این مثال میزان مطالعه متغیر مستقل و توان یادگیری نیز متغیر وابسته است.

اگر محقق در مثال فرضی فوق، به دنبال دانستن این نکته باشد که آیا هوش و جنسیت‌، تأثیرهای متفاوتی در توان یادگیری دانشجویان دارند یا خیر، می‌توان این دو متغیر (هوش و جنسیت‌) را به‌عنوان دو متغیر تعدیل‌ کننده نام برد.

• متغیر کنترل (Control variables)

از آنجایی‌ که متغیر وابسته علاوه بر متغیر مستقل معمولاً از متغیرهای دیگری نیز تأثیر می‌پذیرد بنابراین اگر پژوهشگر بخواهد روابط متغیر وابسته و مستقل را بررسی کند باید سایر متغیرهای تأثیرگذار را به‌ دقت شناسایی و آن ها را به‌ گونه‌ ای کنترل کند که این متغیرها در انجام این تأثیر نداشته باشند. به این دسته از متغیرها که پژوهشگر با روش‌های خاص اثر آنها را خنثی می‌کند متغیرهای کنترل می‌گویند.

• متغیرهای مزاحم و ناخواسته (Disturbing Variables)

در پژوهش به‌ غیراز متغیرهای کنترل متغیرهایی نیز وجود دارند که قابل‌ شناسایی نیستند و به طور ناخواسته بر نتایج تأثیر می‌گذارند به این متغیرها متغیر مزاحم گفته می‌شود.

• رابطه بین متغیرها

از میان سه متغیر متغیرهای مستقل، تعدیل گر و کنترل متغیرهای کنترل حذف شده و فقط متغیرهای مستقل و تعدیل گر مورد بررسی قرار می‌گیرند. متغیرهای وابسته نشان‌ دهنده معلول‌ها یا برونداد ها است و متغیرهای مداخله‌ گر همواره بین علت‌ها و معلول‌ها مداخله می‌کنند.

• سطح سنجش متغیرها

متغیرها از نظر سنجش یا طبقه‌ بندی به چهار دسته: اسمی، رتبه‌ ای یا ترتیبی، فاصله‌ ای و نسبی تقسیم می‌شوند. مقیاس‌های اسمی و رتبه‌ ای مخصوص داده‌ های کیفی هستند و مقیاس‌ های فاصله‌ ای و نسبی مخصوص داده‌ های کمی می‌باشند.

• مقیاس اسمی (nominal scale)

 متغیرهای اسمی متغیرهایی هستند که می‌توان بین طبقات آنها تمایز قائل شد اما نمی‌توان آن ها را رتبه‌ بندی کرد. مثلاً می‌دانیم که افراد متعلق به طبقات مختلف باهم تفاوت دارند اما نمی‌توان میزان آنها را کمی کنیم. در طبقه‌بندی اسمی داده‌ ها بر اساس صفت یا ویژگی گروه‌ بندی می‌شوند.

• مقیاس رتبه‌ ای (ordinal scale)

 این مقیاس‌ها نسبت به مقیاس‌های اسمی پیشرفته‌ تر هستند و در آنها می‌توان شدت و ضعف یک را نیز بررسی کرد. مقیاس رتبه‌ ای برای اندازه‌ گیری متغیرهایی بکار می‌رود که پیوسته هستند. مثلاً برای تعیین رتبه‌ های کنکور می‌ توان مقیاس رتبه‌ ای را بکار برد و افراد را در مراتب: رتبه اول، دوم تا رتبه آخر دسته‌ بندی کرد. از جمله متغیرهایی که در مقیاس رتبه‌ ای کاربرد دارد متغیر نگرش است. در این نوع مقیاس رتبه‌ بندی از عدد کم به بالا انجام می‌گیرد. برای مثال مقیاس‌های لیکرت و فاصله اجتماعی بوگاردوس از این نوع مقیاس هستند.

• مقیاس‌های فاصله‌ ای (Metric scale)

مقیاس‌ های فاصله‌ ای حتی نسبت به مقیاس‌های رتبه‌ ای نیز پیشرفته‌ تر هستند و در آنها می‌توان علاوه بر دارا بودن یک ویژگی یا صفت، مقادیر کمی یا زیادی آنها را نیز مشخص کرد. مقیاس‌های فاصله‌ ای برای داده‌هایی کاربرد دارند که ارزش عددی دارند و می‌توان عملیات ریاضی یا آماری را روی آنها انجام داد. در این مقیاس صفر حقیقی یا مطلق نیست بلکه قراردادی است. مقیاس‌ هایی نظیر دماسنج، آزمون استعداد، آزمون هوش، نمره‌های دانشجویان و نظایر این‌ها از نوع فاصله‌ ای هستند. به‌ طورکلی، مقیاس فاصله‌ ای مقیاسی است که به‌ وسیله آن می‌توان متغیرهای کمی را که دارای مبدأ اختیاری هستند اندازه‌ گیری کرد.

تفاوت های مقیاس اسمی، رتبه ای و فاصله ای

• تبدیل مقیاس رتبه‌ ای به شبه فاصله‌ ای

 زمانی که بخواهیم آزمون‌های آماری را به‌عنوان آزمون فرضیه خود بکار ببریم بسته به شرایط لازم می‌توانیم از آزمون‌های پارامتری قوی‌ تری استفاده کنیم. برای اینکه بتوانیم در مقیاس‌های رتبه‌ ای نیز از آزمون‌های پارامتری استفاده کنیم، باید مقیاس رتبه‌ ای را به مقیاس شبه فاصله‌ ای تبدیل کنیم. برای این کار لازم است ترتیب رتبه‌ بندی را معکوس کرده و به بیشترین ویژگی و صفت بالاترین نمره را اختصاص دهیم.

چه سطحی از سنجش مناسب‌ تر است؟

برای اینکه درک کنید کدام سطح از سنجش مناسب‌ تر است به این نکات توجه کنید:

 داده‌ های عددی را که در قالب گروه‌های خاصی مانند گروه‌ های سنی جمع‌ آوری‌ شده باشند را می‌ توان به داده‌ های فاصله‌ ای تبدیل کرد.

ازآنجایی‌ که مردم معمولاً اطلاعات دقیقی ارائه نمی‌ دهند ممکن است برخی از پرسش‌هایی که نیازمند دقت و جزئیات زیادی هستند غیرقابل‌ اعتماد باشند.

برای متغیرهای فاصله‌ ای، تکنیک‌ های قوی و پیچیده‌ تر تحلیل مناسب است.

به‌ سادگی می‌توان متغیرهایی که در سطح فاصله‌ ای سنجیده شده‌ اند را به سطوح ترتیبی یا اسمی تبدیل کرد ولی داده‌ هایی که در سطوح پایین‌ تر اندازه‌ گیری گردآوری شده‌ اند را نمی‌ توان به سطوح بالاتر تعلیل داد.

• مقیاس نسبی (ratio scale)

مقیاس نسبی دقیق‌ ترین مقیاس سنجش است که در آن علاوه بر تعیین سطوح و مقادیر یک متغیر و فاصله بین مقادیر آن، نسبت‌ها نیز بر اساس صفر حقیقی یا مطلق تعیین می‌ گردند. تمام مقیاس‌ های دقیق فیزیکی نظیر وزن، قد، نیرو، میزان پول و... از این نوع مقیاس هستند.

• آمار توصیفی (descriptive statistics)

آمار توصیفی شامل مجموعه‌ ای از روش‌ها برای سازمان‌ دهی، خلاصه کردن، تهیه جدول، رسم نمودار و... در یک نمونه آماری می‌باشد. این آمار اغلب در قالب آماره‌های توصیفی، جداول یک‌ بعدی، نمودارها، شاخص‌های گرایش به مرکز (مد، میانه و میانگین) و شاخص‌های گرایش به پراکندگی (دامنه تغییرات، واریانس، انحراف استاندارد، چولگی، کشیدگی و چارک بندی) نمایش داده می‌شود.

• آمار استنباطی (inferential statistics)

توسط آمار استنباطی می‌توانیم مشخصات جامعه آماری را از روی نمونه‌ ها استنباط کنیم. به بیان ساده‌تر، آمار استنباطی مشخص می‌کند که آیا الگوها وفرآیندهای کشف شده در نمونه، در جامعه آماری هم کاربرد دارد یا خیر. تفاوت اصلی آمار توصیفی با آمار استنباطی در این است در آمار توصیفی که نتایج مربوطه فقط مختص نمونه‌های مورد بررسی هستند درحالی‌ که در آمار استنباطی نتایج در مورد جامعه بیان می‌شوند.

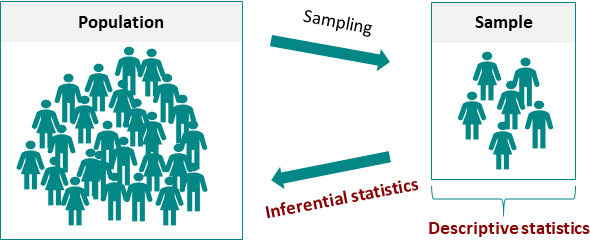
مقایسه آمار توصیفی و آماراستنباطی

• شاخص‌های مرکزی

در آمار، برای اینکه بتوان محل تمرکز داده‌ ها را معرفی کرد از شاخصی به نام شاخص مرکزی استفاده می‌شود. مهم‌ترین شاخص‌ های مرکزی عبارت اند از: مد، میانه و میانگین که به معرفی آن ها می‌پردازیم.

• مد (mode)

به‌ طورکلی می‌توان گفت مد داده‌ ای است که بیشترین فراوانی را دارد. مد ممکن است منحصربه‌ فرد نباشد. مثلاً داده‌های 1،1،2،3،4،1،2،5،7،5،5 دارای دو می‌باشد. این قبیل جامعه ها را دومدی می‌گویند. البته ممکن است یک جامعه چند مدی نیز باشد؛ اما توجه داشته باشید که مد در این قبیل جامعه‌ ها شاخص معتبری نیست؛ زیرا وجود چندین مد نشان‌ دهنده این است که جامعه ما یکدست نیست و لذا اگر مطالعات را دقیق‌ تر کنیم، شاید بتوانیم جامعه را به دو بخش تفکیک کنیم. مثلاً ممکن است در بررسی قد افراد به 2 مد برخورد کنیم که ممکن است نشان‌ دهنده این امر باشد که ما در نمونه‌ گیری بزرگسالان و خردسالان را تفکیک نکرده‌ایم و لذا جامعه‌ ای یکدست نداریم.

در رأی‌ گیری‌ ها اساس تصمیم‌ گیری مد است چون موضوعی که بیشترین فراوانی را داشته باشد، انتخاب می‌شود. در انتخاب رئیس‌ جمهور، نامزدی انتخاب می‌شود که بیشترین رأی (فراوانی) را داشته باشد.

برای محاسبه مد فقط کافی است فراوانی داده هارا باهم مقایسه کنیم و داده با بیشترین فراوانی مد است.

• میانه (median)

 پس از مرتب کردن داده‌ ها، مقداری را که تعداد داده‌ های بعد از آن با تعداد داده‌ های قبل از آن برابر است، میانه می‌نامیم. برای محاسبه میانه ابتدا داده‌ ها را مرتب می‌کنیم. اگر تعداد داده‌ ها فرد باشد، داده‌ ای که در وسط قرار می‌گیرد برابر میانه است و اگر تعداد داده‌ ها زوج باشد نصف مجموع زوج دو داده‌ ای که در وسط قرار گرفته‌ اند برابر میانه است.

• میانگین (mean)

احتمالاً تا اکنون بارها از میانگین برای محاسبه نمرات خود استفاده کرده‌اید. میانگین به‌ طور کلی با نماد x̄ نشان داده می‌شود و معادله آن به این شکل است:

• میانگین وزن‌ دار (weighted mean)

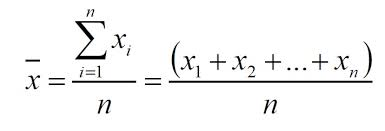
حتماً در طول دوران تحصیلی خود شنیده‌ اید که برخی نمرات شما ضریب دارند. میانگین وزن‌ دار را نیز با نماد x̄ نشان می‌دهند و اگر بخواهند بین میانگین معمولی و میانگین وزن دار تمایز قائل شوند آن را با نماد  W  نشان می‌دهند.

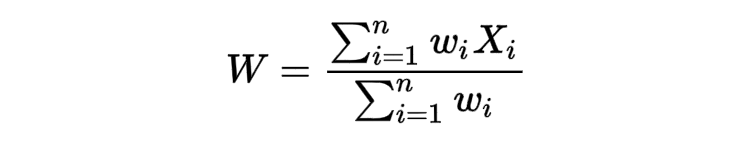
معادله میانگین وزن‌دار

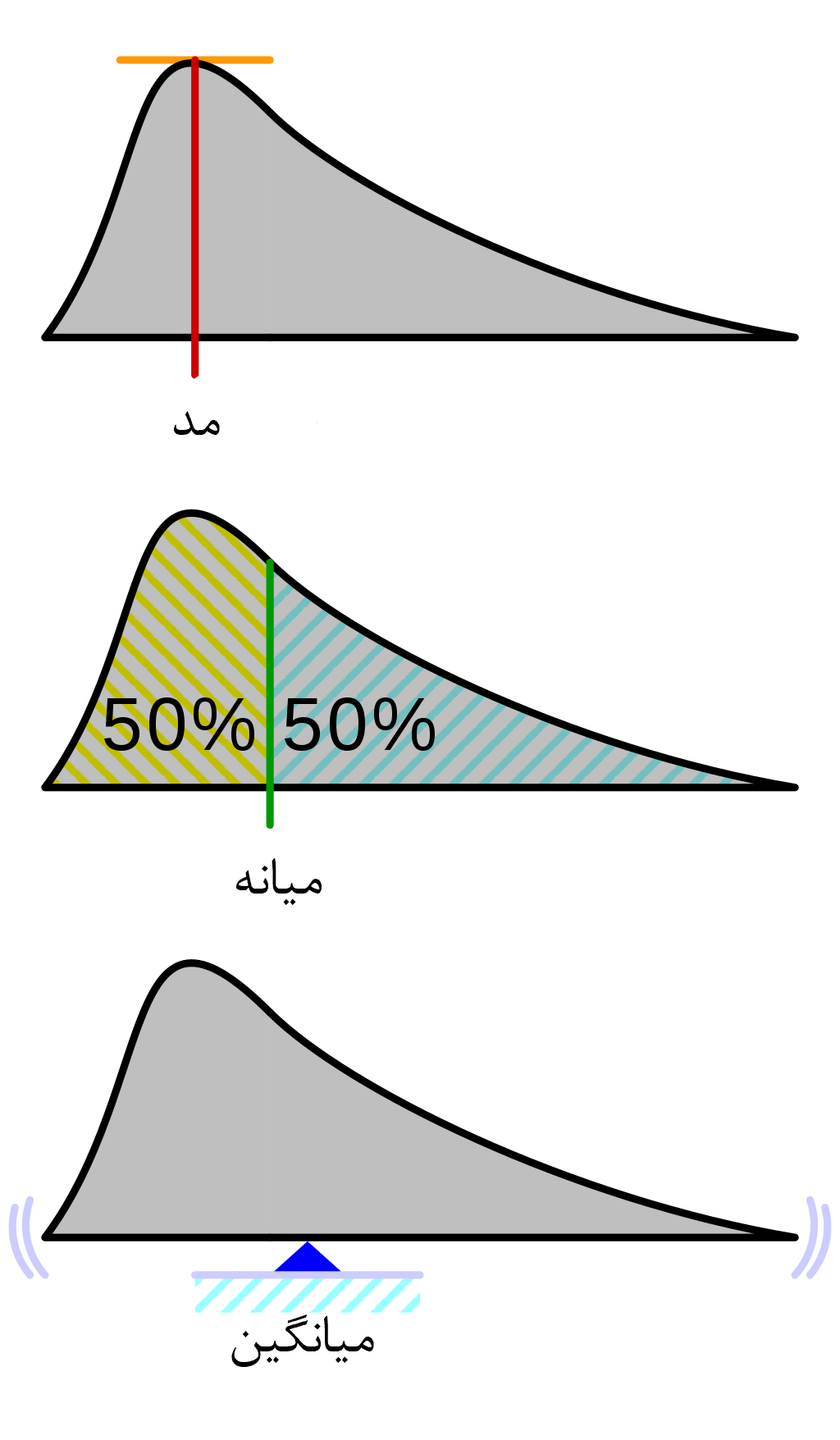
تفاوت میانه، مد، و میانگین

• شاخص‌های پراکندگی (dispersion measures)

معیاری که می‌تواند تفاوت داده‌ ها و میزان این تفاوت‌ ها و به‌ خصوص دوری آن ها از میانگین را اندازه‌ گیری کند شاخص پراکندگی نامیده می‌شود. ما به چند شاخص پراکندگی در زیر اشاره می‌کنیم.

• دامنه تغییرات (range)

طول بازه‌ ای را که متغیر در آن تغییر می‌کند دامنه تغییرات گفته می‌شود و با علامت R نشان داده می‌شود. برای بیان روشن‌ تر فرض کنید: کوچک‌ ترین داده a و بزرگ‌ ترین داده b باشد. پس تفاضل a از b را دامنه تغییرات می‌گویند. هرچقدر داده‌ ها ازهم  دورتر باشند دامنه تغییرات آنها بیشتر خواهد بود و اگر دامنه تغییرات برابر صفر باشد تمام داده‌ ها برابراند. البته بهتر است بدانید دامنه تغییرات در بعضی مواقع به‌ خوبی نمی‌ تواند پراکندگی موجود درداده هارا مشخص کند.

• واریانس (variance)

دامنه تغییرات شاخص مناسبی است؛ اما همان‌ طور گفته شد، این شاخص در تصمیم‌ گیری‌های کلان از ارزش آماری زیادی برخوردار نیست؛ زیرا ما به شاخص‌های نیازی داریم که هم پراکندگی داده‌ها و هم فراوانی آن ها را مد نظر قرار دهند. یک راه ابتدایی این است تک‌ تک مقادیر را از میانگین کم کنیم. به طور خلاصه می‌توان گفت واریانس برابر میانگین مجذور انحرافات از میانگین است و آن را با σ² نشان می‌دهند. معادله واریانس به شکل زیر است:

• انحراف معیار (standard deviation)

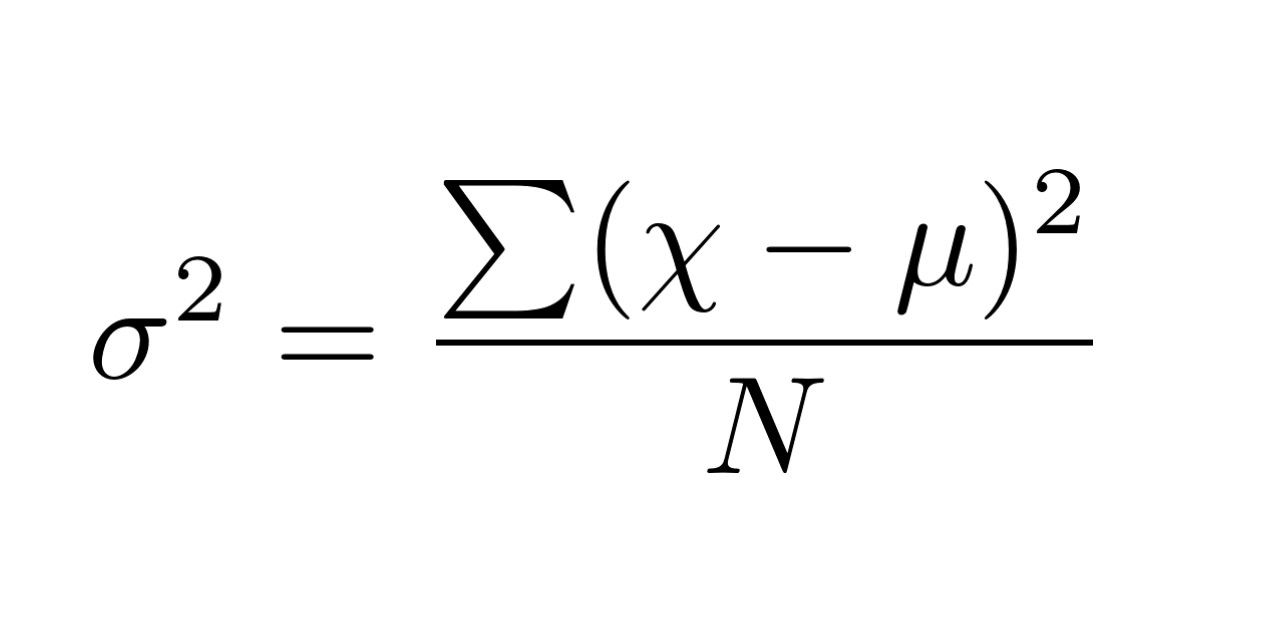
این که واحد واریانس از نوع مجذور واحد متغیر است می‌تواند مشکلات و سو تفاهماتی را در پی داشته باشد. برای اینکه این اختلاف‌نظرها را از بین ببریم سعی می‌کنیم که تفاوت عمده در واحد واریانس و واحد میانگین را با جذر گرفتن از واریانس از بین ببریم. جذر واریانس را انحراف معیار می‌نامیم. انحراف با نماد σ نشان داده می‌ شود و همان‌ طور که گفته شد برابر با جذر واریانس است.

در این مقاله سعی شد به برخی از مفاهیم مهم علم آمار پرداخته شود. اگر این مقاله برای شما مفید لطفاً نظرات خود را با ما به اشتراک بگذارید.

این مقاله در گروه ترجمه، ویرایش و رفع سرقت ادبی ادیت 95 تهیه شده است. استفاده بدون ذکر منبع مجاز نمی‌باشد.

ترجمه و تألیف توسط: فاطمه شوری